Multiphase flow containing non-Newtonian fluids is important in many fields such as the food industry, biological systems, and the recovery of hydrocarbons. It is challenging since the multiphase flow dynamics and the complex rheological properties of the fluids have to be considered simultaneously. For subsurface engineering problems, the interaction between the fluids and the solid porous matrix is also important. This project helps move forward our understanding on this issue by both pore-scale modeling and micromodel experiment.
Many subsurface problems, such as the recovery of hydrocarbons, involve multiphase flow where one of the phases is a non-Newtonian fluid. These fluids exhibit various rheological properties such as the yield stress (the critical stress above which the fluid begin to flow), shear thinning (apparent viscosity decreases with shear rate), shear thickening (apparent viscosity increases with shear rate), viscoelasticity (having both viscous and elastic characteristics), etc. The understanding of multiphase non-Newtonian fluid dynamics is important to these engineering processes. However, the complexity in rheology along with interfacial dynamics makes it difficult to fully predict the mechanisms of multiphase flow of non-Newtonian fluids.
The major goal of this project is to discover the fundamental multiphase non-Newtonian fluid dynamics by using the techniques of pore-scale modeling and micromodel experiments. We have built a micromodel platform and developed two lattice Boltzmann models for multiphase flow (two- and three-phase) of both viscoplastic and viscoelastic fluids.
We have made comprehensive comparisons between the shear-thinning and the shear-thickening fluids for enhanced oil recovery (EOR) using the pore-scale modeling. The performances of shear-thinning and shear-thickening fluids are almost the same when compared in favorable displacement regime (mobility ratio less than 1); while the performance of shear-thinning fluid is poorer than that of shear-thickening fluid in unfavorable displacement regime (mobility ratio greater than 1). These results demonstrate that the shear property of fluids does not play a key role in displacement, but it is still the apparent mobility ratio that controls the displacing efficiency.
We are now focusing on the mechanisms of viscoelasticity on EOR. We have observed the oscillation of a non-wetting droplet when driven by a viscoelastic fluid in a pore-throat microchannel due to the elastic memory effect. Theoretical models have been proposed to predict the oscillation amplitude and frequency. Our lattice Boltzmann modeling has also captured similar behavior, and showed that the elastic-turbulence-induced oscillation would help to release droplets from trapped positions. We will further study the viscoelastic effect in porous media with various wetting conditions.
These works will help the industry to gain better understanding of the roles of non-Newtonian properties in subsurface processes, and to optimize the design of chemicals for EOR.

Multiphase flow in porous media

(a) Newtonian

(b) Viscoelastic
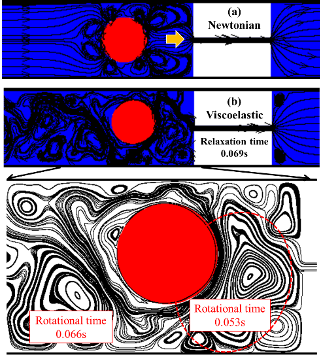
LB simulation shows the oscillation of a droplet driven by a viscoelastic fluid (PRF 2020)
Related publications
- Xie and M.T. Balhoff. Lattice Boltzmann Modeling of the Apparent Viscosity of Thinning-Elastic Fluids in Porous Media. Transport in Porous Media. (under review)
- Xie, K. Xu, K. Mohanty, M. Wang and M.T. Balhoff. Non-wetting droplet oscillation and displacement by viscoelastic fluids. Physical Review Fluids. 5: 063301, 2020
- Xie, W. Lei and M. Wang. Lattice Boltzmann model for three-phase viscoelastic fluid flow. Physical Review E, 97(2): 023312, 2018
- Xie, W. Lv, and M. Wang. Shear-thinning or Shear-thickening Fluid for Better EOR? — A Direct Pore-scale Study. Journal of Petroleum Science and Engineering, 161: 683-691, 2018.
- Xie, J. Zhang, V. Bertola and M. Wang. Lattice Boltzmann Modeling for Multiphase Viscoplastic Fluid Flow. Journal of Non-Newtonian Fluid Mechanics, 234: 118-128, 2016.


